Should I stay or should I go now?
Should I stay or should I go now?
If I go, there will be trouble
And if I stay it will be double
So ya gotta let me know
Should I stay or should I go?
Forty year's later we find ourselves with a trickier trilemma - at the end of every turn you should be asking yourself the question:
Should I stay, snap or go?
Many players coast from turn to turn, going with the flow - perhaps staying in until the end just to see what happens. That approach can certainly lead to some memorable games - so if that appeals don't let us stop you! However if you want to climb the ladder quickly, then figuring out when to snap or retreat is as an essential skill, on par with deck selection and game tactics.
Should I stay on the final turn?
On the final turn the stakes automatically double. Let's say the current stakes are c cubes (about to be doubled to 2c) and you evaluate your probability of winning to be p. (A probability p is just a number between 0 and 1 where 0 represents a 0% chance, 1 represents a 100% chance and e.g. 0.5 represents a 50% chance.)
If you retreat you'll lose c cubes. If you stay, then with probability p you'll earn 2c cubes, and with probability 1-p you'll lose 2c. So on average you'll earn 2c(2p-1) cubes. You are better off staying if this is greater than -c. Manipulating the inequality we see that 2c(2p-1) > -c if and only if p > 1/4.
So if you think you have at least a 25% chance of winning the game, on average it's worth staying in.
(Note that technically you want to consider the probability of ties, but snap.fan data suggests only about 0.4% of games result in a tie, so in practice we can ignore them.)
Should I stay if my opponent snaps?
If your opponent snaps on the final turn, then the stakes if you stay in are quadrupled. This yields the inequality 4c(2p-1) > -c, which means it would be wise to stay in if and only if p > 3/8.
So if you think you have at least a 37.5% chance of winning the game, on average it's worth staying in.
But what should you do if your opponent snaps before the final turn?
It can be tempting to think that this decision is equivalent to the cubes doubling at the end of the game - but this is a flawed way of thinking because if you stay in, the cubes will inevitably double again. If we retreat now we lose c cubes. If we stay we might retreat later and lose 2c cubes, or we might play the game out for 4c cubes. However, we do know that the best thing to do will be to retreat for 2c cubes if we later evaluate our chance of winning as less than 25%, and to stay in otherwise.
So instead of considering the probability of winning from our current position, it can be helpful to break it down into two different decisions. Firstly, what events need to happen (for example, what card do we need to draw) by the final turn for us to then conclude it's still best to stay in. We'll call the probability of those events happening q. Next, what is the probability that we think we'd actually win IF we've decided to stay in on the final turn. We'll call this p'. If our opponent snaps before the final turn we should stay in if and only if:
4cq(2p'-1) - 2c(1-q) > -c
which we can simplify to:
(8p'-2)q > 1
We can visualize this by plotting a nice hyperbolic curve. It's correct to stay in as long as you are in the highlighted red region.
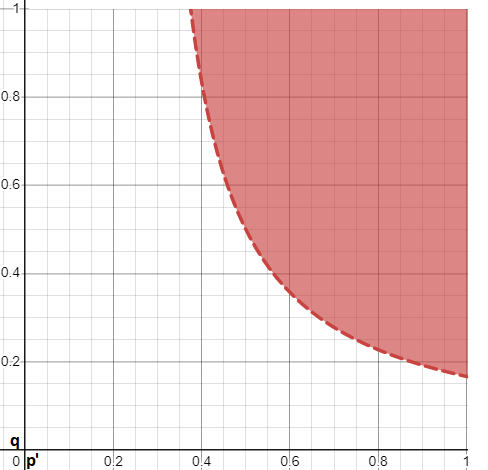
Are you going to be doing all this arithmetic in practice in the middle of a game of Snap? No - probably not. But what rules of thumb can we learn from this?
- If there is nothing that could possibly happen before the final turn to increase your chance of winning to at least 37.5%, then you should retreat now.
- If it's turn 5, and you think the only way you win is to draw one of your 4 remaining cards, then you want to be at least 75% sure you will actually win if you draw that card.
- If you are hoping for a certain set of circumstances to occur before the final turn in order to have a chance of winning, those circumstances should have AT LEAST a 1 in 6 chance of occurring. (And if it's only 1 in 6, you should be certain you'll win if they do occur.)
As a wibbly-wobbly corollary to this, if my opponent snaps, then if my only out is reliant on TWO things happening, (e.g. me drawing a card AND them not drawing their key card), it's usually best to retreat.
Should I snap?
So far we've only scratched the surface. The analysis becomes more fun once we throw snapping into the mix. We'll cover this in a later guide. However to vastly oversimplify things... If you think you have a greater than 50% chance of winning, why not snap and raise the stakes?
Should I adjust my play against bots?
When to snap against bots is an interesting question; however when to retreat against them is relatively straightforward. The arithmetic doesn't really change. The only thing to note is that our current best hypothesis is that the bots are only using the state of the board to make their own snapping decisions. Since all this information is already known to you this means that there isn't really much to learn from a bot's decision to snap or not. Unlike playing against a human, who will be much more likely to use the state of their hand to inform their decision.
Should I retreat now or retreat later?
In theory retreat later is the better option. If you retreat now you always lose cubes, but there is a chance that if you retreat later - your opponent may also retreat and the game end in a tie. In practice it would be unusual for both players to evaluate that retreating is correct - and there's definitely a time cost to waiting. Looking at matches uploaded to snap.fan, we see that when one player concedes, there's only a 0.6% chance that the other player will also concede. On average retreat later extends the game by several seconds. From my own data I'd estimate that I will have saved about 24 cubes over the entire course of the closed beta by using retreat now, but would have earnt about 108 cubes if I'd used that time to play more games.
Some players suggest waiting until the time almost runs out before selecting retreat now. That way if your opponent uses retreat now, you win rather than tie. For general ladder play this is almost certainly bad advice. In some cases you are extending your games by almost a minute to gain a tiny fraction of an edge. The opportunity cost of earning cubes by playing more games means this just isn't worth it.
How do I estimate my probability of winning?
All of the above relies on you being able to somewhat accurately estimate your probability of winning. This is a very complex skill-testing element of Marvel Snap. There are several factors to account for:
- What is left in your deck and how likely are you to draw it?
- Given the cards you've already observed them play, what else is your opponent likely to have?
- Where will your opponent commit their power? Is it obvious, or are we about to play a shell game?
- Given my opponent has decided to stay in or snapped, what does that tell me about their hand? (Try putting yourself in their position... what sort of things would cause you to snap?)
Combining all of that information into a probability of victory is tricky and worth exploring in more depth. My advice is to get into the habit of putting a number to it, and then observing the outcome. If you stay on top of this you'll quickly learn whether you tend to under or overestimate. Adapt your estimates accordingly and you'll become more accurate. Become more accurate and you'll make better decisions. Make better decisions and you'll climb the ladder faster.
Caveats
In this guide we assume that you are playing ladder and your goal is to climb quickly by maximizing your expected number of cubes per game. If you are competing in the newly announced battle format (where the goal is to get 10 cubes before your opponent), or in a competitive format such as Cube Rush (where the goal is to get more cubes than all your opponent's in 60 minutes), maximizing cubes per game isn't necessarily the thing you should be optimizing.

